Using awkward arrays to analyze HEP data
Last updated on 2024-12-16 | Edit this page
Estimated time: 20 minutes
Overview
Questions
- What are awkward arrays?
- How do I work with awkward arrays?
Objectives
- Learn to use awkward arrays in a simple, naive way.
- Learn to use awkward arrays in a much faster way, making use of the built-in functionality of the library.
Why awkward?
A natural question to ask would be “Why do I have to learn about awkward? Why can’t I just use numpy?” And yes, those are two questions. :) The quick answers are: you don’t have to and you can! But let’s dig deeper.
Awkward-array is a newer python tool written by Jim Pivarski (Princeton) and others that allows for very fast manipulation of ``jagged” arrays, like we find in HEP. You definitely don’t have to use it, but we present it here because it can speed things up considerably…if you know how to write your code.
Similarly, you can of course use standard numpy arrays
for many parts of your analysis, but your data may not always fit into
numpy arrays without some careful attention to your code.
In either case, you’ll want to think about how to work with your data
once you get it out of your file.
Environment
Use the Python environment that you set up in the previous two lesson pages. We leave it up to you whether or not you write and execute this code in a script or as a Jupyter notebook.
Numpy arrays: a review
Before we dive into awkward lets review some of the
awsome aspects of numpy arrays…and also examine their
limitations.
Let’s import numpy (if you have not already done that in
this python session).
Next, let’s make a simple numpy array to use for our
exmples.
OUTPUT
[1 2 3 4]Numpy arrays are great because we can perform mathematical operations on them and the operation is quickly and efficiently carried out on every member of the array.
PYTHON
y = 2*x
print(y)
print() # This just puts a blank line between our other print statements
z = x**2
print(z)
print()
a = np.sqrt(x)
print(a)OUTPUT
[2 4 6 8]
[ 1 4 9 16]
[1. 1.41421356 1.73205081 2. ]Note that in that last operation where we take the square root, we
made use of a numpy function sqrt. That
function
`knows" how to operate on the elements of a numpy array, as opposed to the standard pythonmathlibrary which does *not* know how to work withnumpy`
arrays.
So this seems great! However, numpy arrays break down
when you have arrays that are not 1D and cannot be expressed in a
regular
`n x m" format. For example, suppose you have two events and each event has two muons and you want to store the transverse momentum ($p_T$) for these muons in anumpy`
array.
OUTPUT
[[ 20.9 12.3]
[127.1 60.2]]
[[ 41.8 24.6]
[254.2 120.4]]Great! Everything looks good and we get our expected behavior!
Now, suppose there are 3 muons in the second event. Does this still work?
OUTPUT
[list([20.9, 12.3, 20.9, 12.3])
list([127.1, 60.2, 23.8, 127.1, 60.2, 23.8])]Wait…what??? It looks like it just duplicated the entries so now it
looks like we’re storing information for 4 muons in the first
event and 6 muons in the second event! A closer looks shows us
that while pt is a numpy array, the elements
are not arrays but python list objects, which behave
differently.
The reason this happened is that numpy arrays can’t deal
with this type of
`jagged" behavior where the first row of your data might have 2 elements and the second row might have 3 elements and the third row might have 0 elements and so on. For that, we needawkward-array`.
Access or download a ROOT file for use with this exercise
We’ll work with the same file as in the previous lesson. If you have jumped straight to this lesson, please go back and review how to access the file over the network or by downloading it.
Open the file
Stop!
If you haven’t already, make sure you have run through the previous lesson on working with uproot.
Let’s open this ROOT file! If you’re writing a python script, let’s
call it open_root_file_and_analyze_data.py and if you’re
using a Jupyter notebook, let’s call it
open_root_file_and_analyze_data.ipynb.
First we will import the uproot library, as well as some
other standard libraries. These can be the first lines of your python
script or the first cell of your Jupyter notebook.
If this is a script, you may want to run
python open_root_file_and_analyze_data.py every few lines
or so to see the output. If this is a Jupyter notebook, you will want to
put each snippet of code in its own cell and execute them as you go to
see the output.
PYTHON
import numpy as np
import matplotlib.pylab as plt
import time
import uproot
import awkward as akLet’s open the file and pull out some data.
PYTHON
# Depending on if you downloaded the file or not, you'll use either
infile_name = 'root://eospublic.cern.ch//eos/opendata/cms/derived-data/AOD2NanoAODOutreachTool/ForHiggsTo4Leptons/SMHiggsToZZTo4L.root'
# or
#infile_name = 'SMHiggsToZZTo4L.root'
# Uncomment the above line if you downloaded the file.
infile = uproot.open(infile_name)
events = infile['Events']
pt = events['Muon_pt']
eta = events['Muon_eta']
phi = events['Muon_phi']Let’s inspect these objects a little closer. To access the actual
values, we’ll see we need to use the .array() member
function.
PYTHON
print(pt)
print()
print(pt.array())
print()
print(len(pt.array()))
print()
for i in range(5):
print(pt.array()[i])OUTPUT
<TBranch 'Muon_pt' at 0x7f01513a5c88>
[[63, 38.1, 4.05], [], [], [54.3, 23.5, ... 43.1], [4.32, 4.36, 5.63, 4.75], [], []]
299973
[63, 38.1, 4.05]
[]
[]
[54.3, 23.5, 52.9, 4.33, 5.35, 8.39, 3.49]
[]Taking a closer look at the entries, we see different numbers of values in each ``row”, where the rows correspond to events recorded in the CMS detector.
So can we use manipulate this object like a numpy array? Yes! If we’re careful about accessing the array properly.
OUTPUT
[[126, 76.2, 8.1], [], [], [109, 47, 106, 8.66, 10.7, 16.8, 6.98], []]When we histogram, however, we need to make use of the
awkward.flatten function. This turns our
awkward array into a 1-dimensional array, so that we lose
all record of what muon belonged to which event.
PYTHON
print(ak.flatten(pt.array()))
plt.figure()
plt.hist(ak.flatten(pt.array()),bins=100,range=(0,100));
plt.xlabel(r'Muon $p_T$ (GeV/c)',fontsize=14)OUTPUT
[63, 38.1, 4.05, 54.3, 23.5, 52.9, 4.33, ... 32.6, 43.1, 4.32, 4.36, 5.63, 4.75]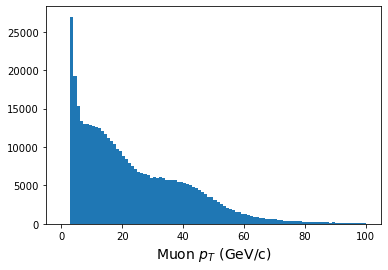
We can also manipulate the data quite quickly. Let’s see how!
This sample file is Monte Carlo data that simulates the decay of Higgs bosons to 4 charged leptons. Let’s look for decays to 4 muons, where there are two positively charged muons and 2 negatively charged muons.
Since the data stores momentum information as \(p_T, \eta, \phi\), first we’ll calculate the Cartesian \(x,y,z\) components of momentum, and then we’ll loop over our events to calculate an invariant mass. We’ll find that looping over the entries is slow, but there is a faster way!
First the slow but explicit way:
PYTHON
# Some helper functions
def energy(m, px, py, pz):
E = np.sqrt( (m**2) + (px**2 + py**2 + pz**2))
return E
def invmass(E, px, py, pz):
m2 = (E**2) - (px**2 + py**2 + pz**2)
if m2 < 0:
m = -np.sqrt(-m2)
else:
m = np.sqrt(m2)
return m
def convert(pt, eta, phi):
px = pt * np.cos(phi)
py = pt * np.sin(phi)
pz = pt * np.sinh(eta)
return px, py, pz
# Convert momentum to x,y,z components
muon_number = events['nMuon'].array()
pt = events['Muon_pt'].array()
eta = events['Muon_eta'].array()
phi = events['Muon_phi'].array()
muon_q = events['Muon_charge'].array()
mass = events['Muon_mass'].array()
muon_px,muon_py,muon_pz = convert(pt, eta, phi)
muon_e = energy(mass, muon_px, muon_py, muon_pz)
# Do the calculation
masses = []
nevents = len(pt)
print(f"Nevents: {nevents}")
start = time.time()
for n in range(nevents):
if n%10000==0:
print(n)
nmuons = muon_number[n]
e = muon_e[n]
q = muon_q[n]
px = muon_px[n]
py = muon_py[n]
pz = muon_pz[n]
if nmuons < 4:
continue
for i in range(0, nmuons-3):
for j in range(i+1, nmuons-2):
for k in range(j+1, nmuons-1):
for l in range(k+1, nmuons):
if q[i] + q[j] + q[k] + q[l] == 0:
etot = e[i] + e[j] + e[k] + e[l]
pxtot = px[i] + px[j] + px[k] + px[l]
pytot = py[i] + py[j] + py[k] + py[l]
pztot = pz[i] + pz[j] + pz[k] + pz[l]
m = invmass(etot, pxtot, pytot, pztot)
masses.append(m)
print(f"Time to run: {(time.time() - start)} seconds")
# Plot the results
plt.figure()
plt.hist(masses,bins=140,range=(80,150))
plt.xlabel(r'4-muon invariant mass (GeV/c$^2$',fontsize=18)
plt.show()
When I run this on my laptop, it takes a little over 3 minutes to run. Is there a better way?
Yes!
We’ve adapted some code from this tutorial, put together by the HEP Software Foundation to show you how much faster using the built-in awkward functions can be:
PYTHON
start = time.time()
muons = ak.zip({
"px": muon_px,
"py": muon_py,
"pz": muon_pz,
"e": muon_e,
"q": muon_q,
})
quads = ak.combinations(muons, 4)
mu1, mu2, mu3, mu4 = ak.unzip(quads)
mass_fast = (mu1.e + mu2.e + mu3.e + mu4.e)**2 - ((mu1.px + mu2.px + mu3.px + mu4.px)**2 + (mu1.py + mu2.py + mu3.py + mu4.py)**2 + (mu1.pz + mu2.pz + mu3.pz + mu4.pz)**2)
mass_fast = np.sqrt(mass_fast)
qtot = mu1.q + mu2.q + mu3.q + mu4.q
print(f"Time to run: {(time.time() - start)} seconds")
plt.hist(ak.flatten(mass_fast[qtot==0]), bins=140,range=(80,150));
plt.xlabel(r'4-muon invariant mass (GeV/c$^2$',fontsize=18)
plt.show()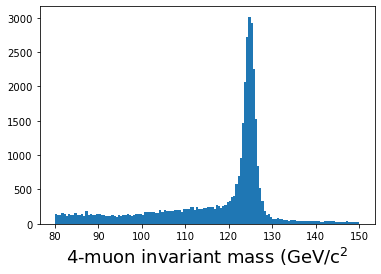
On my laptop, this takes less than 0.2 seconds! Note that we are
making use of boolean
arrays to perform masking when we type
mass_fast[qtot==0].
While we cannot teach you everything about
awkward, we hope we’ve given you a basic introduction to
what it can do and where you can find more information so that you can
quickly process the output of any of your open data jobs and get started
on your own analysis!
- Awkward arrays can help speed up your code, but it requires a different way of thinking and more awareness of what functions are coded up in the awkward library.
